Deal or No Deal: Graphing a Binary Rev Challenge
This post will describe solving a challenge from BYU Capture the Flag 2024. The challenge was called Deal or No Deal and was in the rev category.
A compiled Rust binary is provided. Binary Ninja wasn’t great at handling this sample, so I used Ghidra instead. Following the entry point leads us to the main function of the Rust program, which looks like:
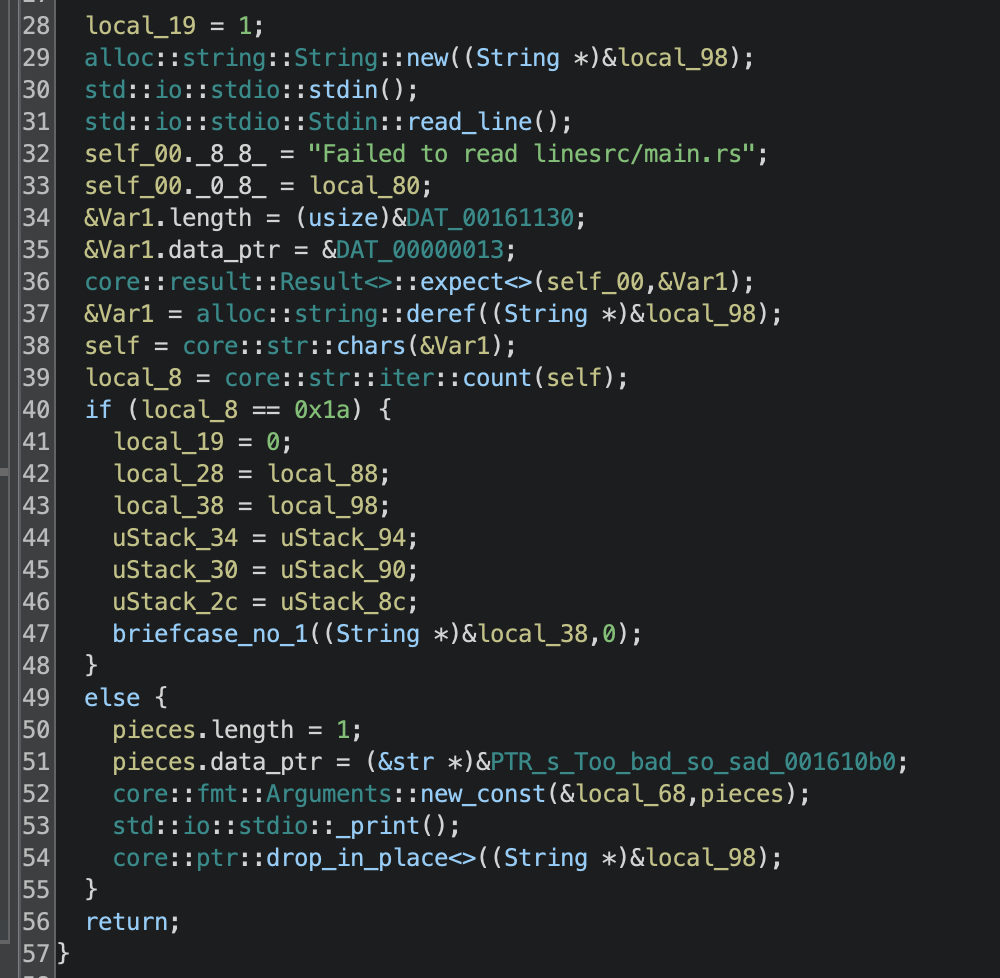
So it reads a line from stdin, then counts the number of characters. If the input is 26 chars long then it calls briefcase_no_1 with the input string and the value 0, otherwise it prints out the message “Too bad so sad”. This tells us that the flag we are looking for is 25 characters long, as the last character will be \n.
The briefcase_no_1 function first prints out a message letting us know that we are opening the first briefcase, then accesses the first character of the provided input string parameter, storing it in a variable named cVar1. Next it creates a new string via skipping the first character of the input, then has a series of if statements that match the first character we accessed and the value of the no parameter:
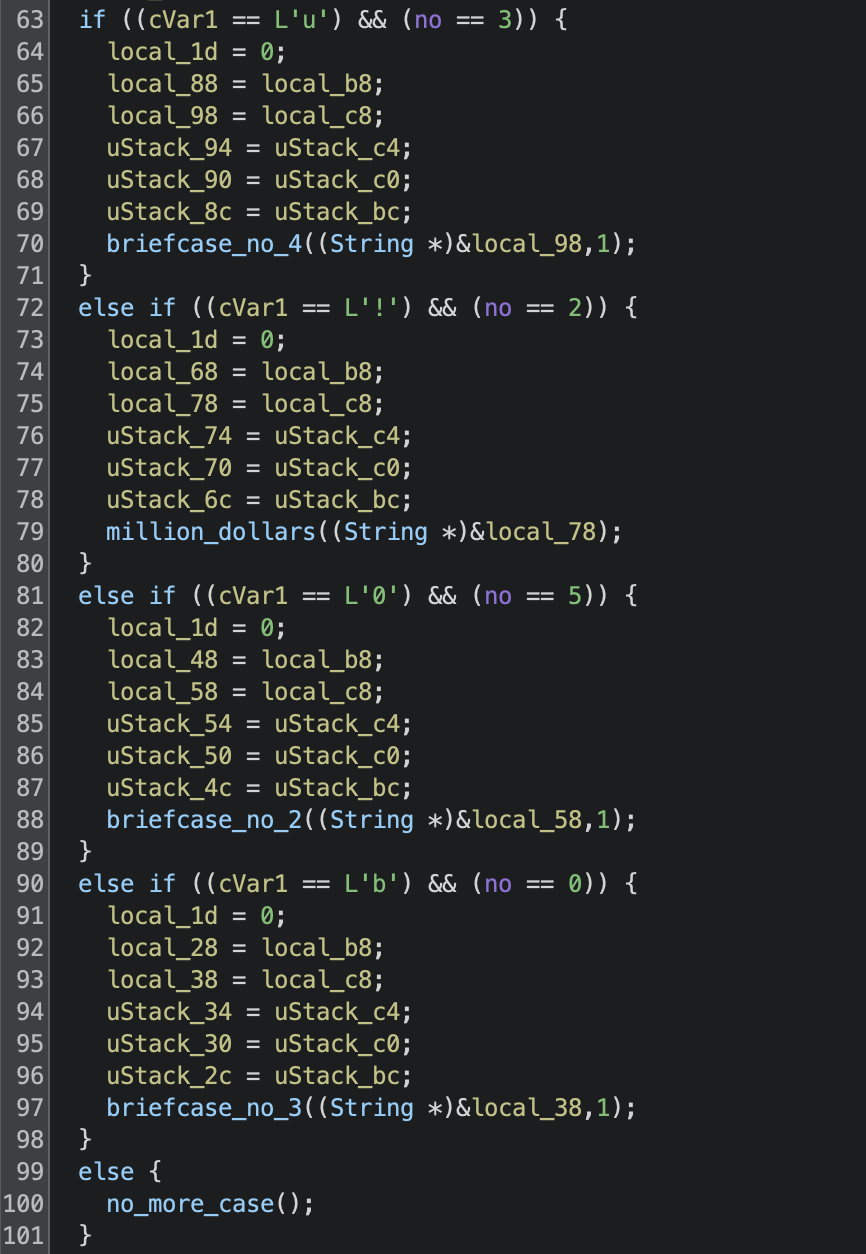
If one of these conditions is met, it calls another briefcase function with the new string we created and another no value, or in one case a function named million_dollars. Otherwise it calls a function called no_more_case, which simply just prints out the same error message “Too bad so sad”.
If we look at the other briefcase functions, they all follow a similar pattern. This seems like checking the flag character by character, and taking a different path through the functions depending on each character.
Recall the main function called briefcase_no_1 with the original string and the value 0. The last if statement checks for the first character being b and no being 0, which matches up with the expected flag format byuctf{...}.
The million_dollars function simply checks for the next character being } and if so prints that we have won, otherwise lets us know we were so close:
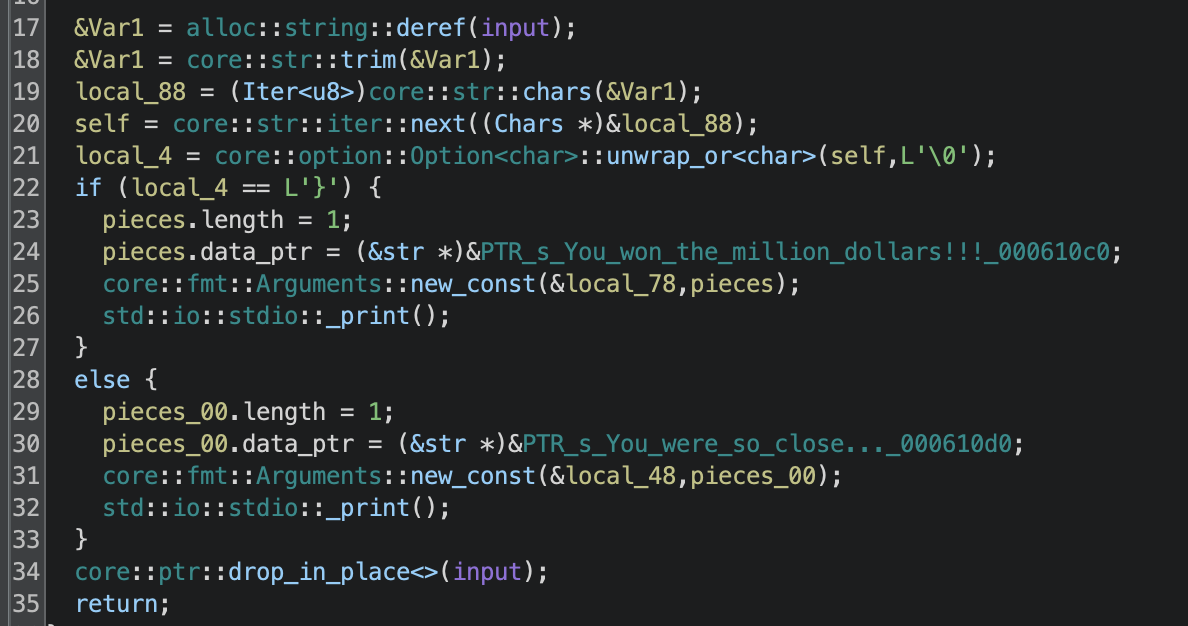
So if we can find 24 characters that lead us to the million dollars, plus } at the end, then we have the flag. We can just follow through these function calls, matching the next character each time. However it’s not so simple, as in many cases there are several conditions checking for the same no value but different characters, so the next character isn’t always as easily identifiable.
However I already knew the start of the flag, and luckily the flag actually spelled something out (in leetspeak), so during the CTF I was able to follow along manually and obtain the flag character by character via a process of educated guessing and backtracking whenever I got a character wrong. This revealed the flag
byuctf{y0u_cAn_uS3_rust!}
Automating it
This manual process worked fine in this case, but what if the flag hadn’t spelled anything out, or it had been hundreds of characters long. Or even worse, the functions could have had lots of fake paths and loops that only lead to a failure state after hundreds of characters. To be able to handle that, we would need to completely automate the process.
To do this I thought of it as a graph problem: with each briefcase function and no combination being a node, and the calls to other briefcase functions being the edges between them. If we label each edge with the character it matched, then finding a path from the start to the end node of the desired length will give us the flag.
I wrote a script using the Ghidra API (using the headless analyzer tool to avoid needing the GUI), to parse out the nodes and edges and build the graph. The script operated at the instruction level and is fairly long so I won’t show it, but it can be found here.
The graph obtained looks like:
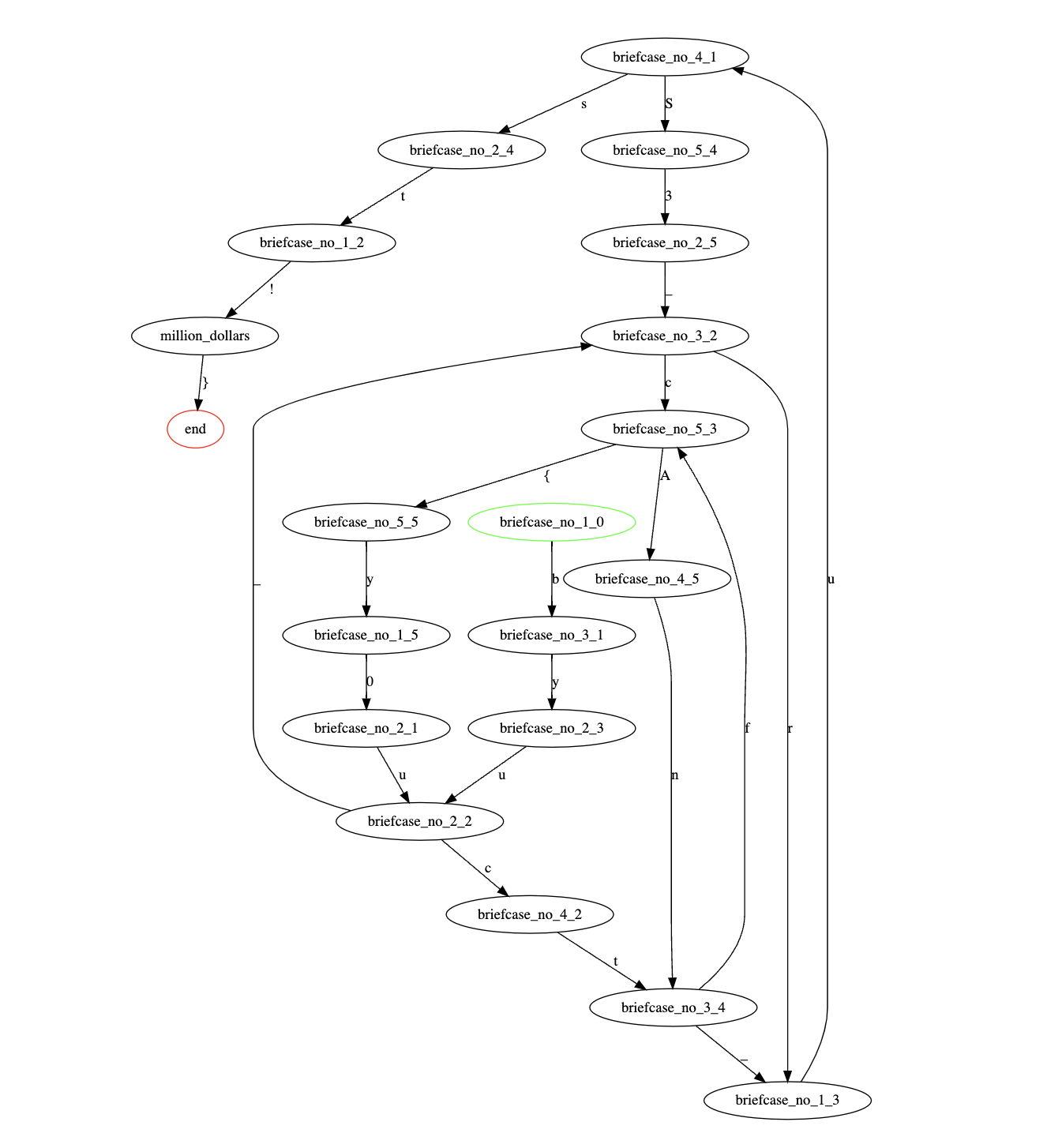
The start and end nodes are green and red respectively, and the characters are displayed on each edge. Interestingly, there actually are multiple loops present. Now we can just use any path finding algorithm to find a path of length 25 from the start to end node.
Doing so reveals that there are actually 26 such paths that satisfy. The according strings are
byu_c{y0u_c{y0u_cAn_ust!}
byu_c{y0u_cAnf{y0u_rust!}
byu_c{y0u_cAnfAnfAn_ust!}
byu_c{y0uctfAn_uS3_rust!}
byu_c{y0uct_uS3_cAn_ust!}
byu_cAnf{y0u_c{y0u_rust!}
byu_cAnf{y0u_cAnfAn_ust!}
byu_cAnf{y0uct_uS3_rust!}
byu_cAnfAnf{y0u_cAn_ust!}
byu_cAnfAnfAnf{y0u_rust!}
byu_cAnfAnfAnfAnfAn_ust!}
byu_cAn_uS3_c{y0uct_ust!}
byu_ruS3_c{y0uctfAn_ust!}
byu_ruS3_cAnf{y0uct_ust!}
byu_ruS3_ruS3_ruS3_rust!}
byuctf{y0u_cAn_uS3_rust!}
byuctf{y0u_ruS3_cAn_ust!}
byuctf{y0uctf{y0uct_ust!}
byuctfAnf{y0u_ruS3_rust!}
byuctfAnfAnfAn_uS3_rust!}
byuctfAnfAn_uS3_cAn_ust!}
byuctfAn_uS3_c{y0u_rust!}
byuctfAn_uS3_cAnfAn_ust!}
byuct_uS3_c{y0u_cAn_ust!}
byuct_uS3_cAnf{y0u_rust!}
byuct_uS3_cAnfAnfAn_ust!}
That’s strange, I was only expecting one solution. The correct flag that we found before, byuctf{y0u_cAn_uS3_rust!}, is present in the list so clearly the approach was correct.
I tried passing one of the other strings we found to the binary, and interestingly it worked.
Trying some of the other strings yields the same result, so all of them are correct solutions. I’m not sure whether the author meant to include more than one correct input, or left them in as an Easter egg. Either way you could have identified the flag as it was the only one which met the expected format and also spelt out something meaningful. Pretty interesting.
Epilogue
The source code for the challenge can be found here.
The Ghidra script for building the graph and path finding can be found here.